How many edges meet at each vertex?
You’ve probably heard the terms “edges” and “vertices” before, maybe in geometry class. Let’s take a closer look at what they mean and how they relate to each other. Edges are the straight lines that make up the sides of the polygons that form a shape’s faces. A vertex (or corner) is a point where at least three edges come together.
Think of a cube. Each corner is a vertex, and three edges meet at each vertex. Now imagine a pyramid. The pyramid’s tip is a vertex, and four edges meet at that point. This is why we say at least three edges meet at a vertex – there can be more!
Let’s take this a step further. In a cube, each face is a square. Squares have four sides, and each side is an edge. Since each vertex of the cube is formed by three edges, it’s easy to see how the cube has 12 edges (4 edges per square x 6 squares = 24, and we divide by 2 because each edge is shared by two squares = 12).
But things get a little more interesting with shapes that aren’t as straightforward as a cube. Think about a soccer ball. Each face is a pentagon or a hexagon. A pentagon has five sides, and a hexagon has six. To figure out how many edges meet at each vertex, you’d have to count the number of sides on each polygon surrounding the vertex. It might seem complex, but the idea is the same: edges form the sides of the polygons that make up a shape, and vertices are the points where those edges meet.
Understanding the relationship between edges and vertices is key to grasping the structure of any three-dimensional shape. It helps us see how the various parts of a shape come together and form a cohesive whole.
How does cuboid have 12 edges?
A cuboid, also known as a rectangular prism, is a three-dimensional shape with six rectangular faces. It’s essentially a box! Each face has four edges, and there are three pairs of opposite faces. Since each edge is shared by two faces, we can calculate the total number of edges by multiplying the number of edges per face by the number of faces and then dividing by two. This gives us (4 * 6) / 2 = 12edges.
Think of it like this: Imagine you’re building a box with six pieces of cardboard. Each piece of cardboard has four sides. These sides are the edges of the box. When you put all the pieces together, some of the sides will overlap. This overlapping is why we divide by two in the calculation.
The formula you mentioned, 6 + 8 − 12 = 2, is actually a mathematical concept called Euler’s Formula. This formula applies to any polyhedron (a three-dimensional shape made up of polygons) and relates the number of faces (F), vertices (V), and edges (E) of the polyhedron. The formula states that F + V − E = 2. In the case of a cuboid, this formula confirms that it has six faces (F = 6), eight vertices (V = 8), and 12edges (E = 12), because 6 + 8 − 12 = 2.
Essentially, Euler’s Formula helps us understand the relationship between the number of faces, vertices, and edges of any polyhedron. It’s a useful tool for verifying the characteristics of these shapes and can help us visualize their structure.
What is a vertex on a cuboid?
Let’s break down why a cuboid has eight vertices:
Cuboids are like rectangular boxes, having six rectangular faces.
* Each face has four vertices.
* Since there are six faces, and each face contributes four vertices, that means there are a total of 24 vertices. However, every vertex is shared by three different faces. Therefore, we divide 24 by 3 to get 8. This is how we arrive at the fact that a cuboid has 8 vertices.
It’s easy to visualize this. Imagine a shoebox: each corner of the box is a vertex. You can count eight of these vertices, one for each corner of the box. This is a simple example, but it helps us understand how vertices contribute to the overall shape of a cuboid.
How many edges are on a cuboid?
Let’s break down the concept of edges in a cuboid. Imagine a cube, which is a special type of cuboid where all sides are equal. Each side of the cube has 4 edges. Since a cube has 6 sides, it has a total of 24 edges. However, you’ll notice that each edge is shared by two sides. Therefore, you divide 24 by 2 to get the final count of 12 edges.
You can apply the same logic to any cuboid, even if the sides are not equal. The key is understanding that each edge is a line segment connecting two vertices. Counting the number of edges on a cuboid is a simple task once you visualize the shared nature of the edges between the faces.
How many edges of a cuboid meet a vertex?
Let’s break this down a little further. Imagine a cuboid, like a shoebox. Each corner of the shoebox is a vertex. Now, picture the lines where the sides of the box meet. These lines are called edges. If you look at any single corner (vertex), you’ll see three edges coming together at that point.
Think of it like this: Each vertex is where three faces of the cuboid intersect. Since each face has an edge, the point where the three faces meet is also the point where three edges meet.
Can an edge have only 1 vertex?
But don’t worry, the world of mathematics is full of exciting possibilities! We can explore different types of graphs. For example, a loop is a special kind of edge that connects a vertex to itself. Think of it like a closed circle, where the start and end point are the same. This way, we can have an edge that seems to have only one vertex.
But even loops still connect two vertices, even if they are the same. You might be wondering, can we have a half-edge? It’s a concept that some might find interesting, but it doesn’t have a place in the world of standard graph theory.
Imagine a graph as a map, and vertices as cities, and edges as roads. In a standard map, a road always connects two cities, right? You can’t have a road that starts at a city but doesn’t lead to another one. That’s kind of like a half-edge, and it doesn’t quite fit into the usual map or graph framework.
If we want to explore half-edges, we need to think about how we would define them mathematically. It’s a bit of a challenge, but a very interesting one! It could lead to new and exciting concepts and possibilities in the study of graphs.
What cuboid has 8 vertices and 12 edges?
Think about a box. A box is a great example of a cuboid. It has six sides, eight corners, and twelve edges. Each corner is called a vertex, and each line where two faces meet is called an edge. A cube is a special kind of cuboid where all the sides are the same length. Think about a dice. A dice is a cube! It has six sides that are all squares, and all the sides are the same size.
See more here: How Does Cuboid Have 12 Edges? | How Many Edges Of A Cuboid Meet In A Vertex
How many vertices does a cuboid have?
Now, let’s delve a little deeper. Vertices are really important when it comes to understanding geometry. They help us define the shape and size of things. For example, if we wanted to know the volume of a cuboid, we’d need to know the length, width, and height. But, to even measure those things, we need to understand where those edges meet – that’s where our vertices come in!
Think about it this way. You can’t really have a cuboid without vertices! They’re the building blocks that hold everything together. And, since a cuboid has eight vertices, that’s just the way it is!
How many edges are in a cuboid?
Let’s take a closer look. Imagine you have a box, like a shoebox. This box is a cuboid. Count all the straight lines that make up the box. You’ll find there are twelve of them. Each of these lines is an edge.
You can also think of it this way: A cuboid has six faces, and each face has four sides. Since each side is shared by two faces, we divide the total number of sides (24) by two to get the number of edges (12). This gives us twelve edges in a cuboid.
What is the relation between face vertices and edges of a cuboid?
Let’s apply this to our cuboid. It has six faces, eight vertices, and twelve edges. Plugging these values into Euler’s formula, we get 6 + 8 = 12 + 2, which simplifies to 14 = 14. This confirms that Euler’s formula holds true for the cuboid!
Now, let’s break down the connection between these elements a bit more. Think of the vertices as the corners of the cuboid. Each vertex is where three edges meet. Each face is surrounded by edges, and these edges connect the vertices.
Here’s a helpful visualization: imagine you’re building a cardboard box. You start with six rectangular pieces of cardboard (the faces). You then fold these pieces to create the box, attaching the edges of each piece to the edges of other pieces. This folding process creates the vertices where the edges meet.
The beauty of Euler’s formula is that it captures this fundamental relationship between faces, vertices, and edges for any polyhedron, not just the cuboid. So, next time you see a pyramid, a prism, or any other 3D shape, remember that Euler’s formula helps connect the dots (or rather, the vertices, edges, and faces) of the shape.
How many faces does a cuboid have?
Let’s dive into the details. Cuboids have six faces, which are just flat surfaces. Think of them like the sides of a box. Each face is a rectangle, and they all come together to make a closed, three-dimensional shape. You can also imagine cuboids as having eight vertices, which are like the corners of the box. And, they have twelve edges, which are the lines where the faces meet.
Think of it this way: Imagine a cuboid as a building. The walls are the faces, the corners are the vertices, and the edges are the lines where the walls meet. Pretty cool, right?
So, if you’re ever looking at a cuboid, just remember that it has six faces, eight vertices, and twelve edges! It’s a pretty simple shape, but it’s definitely a cool one.
See more new information: linksofstrathaven.com
How Many Edges Of A Cuboid Meet At A Vertex?
The answer is three.
Think of a cuboid like a box. Each corner of the box is a vertex. And at each vertex, three edges come together.
Let’s break it down a bit further. A cuboid is a three-dimensional shape with six rectangular faces. Each face has four edges. So, if you count all the edges of the cuboid, you’ll find there are 12 edges in total.
Now, imagine you’re looking at one vertex of the cuboid. This vertex is where three faces of the cuboid meet. Each of those faces contributes one edge to the vertex, and that’s how you get three edges meeting at a single vertex.
Visualizing the Cuboid
It can be helpful to visualize this. Imagine holding a box in your hand. Pick one corner of the box. You’ll see that three edges of the box are coming together at that corner. That’s your vertex!
Why It Matters
Understanding the relationship between vertices, edges, and faces of a cuboid is a foundational concept in geometry. It’s essential for understanding more complex geometric shapes and solving problems related to volume, surface area, and angles.
Let’s Talk Terminology
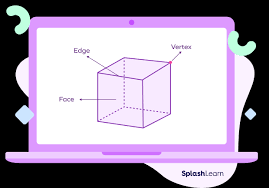
Vertex: A vertex is a point where two or more lines, edges, or sides meet. It’s essentially a corner.
Edge: An edge is a line segment that connects two vertices. Think of it as a side.
Face: A face is a flat surface that makes up part of a three-dimensional shape.
More About Cuboids
A cuboid is also called a rectangular prism. It’s a special type of prism where all the faces are rectangles. A cube is a special type of cuboid where all the faces are squares.
Beyond the Cuboid
This concept of vertices, edges, and faces isn’t limited to cuboids. It applies to other three-dimensional shapes as well, like pyramids, cones, spheres, and cylinders.
Let’s say you have a pyramid. A pyramid has a base and triangular faces that meet at a point called the apex. The apex is a vertex, and you’ll find that multiple edges meet at this vertex.
FAQs
Q: How many vertices does a cuboid have?
A: A cuboid has eight vertices. Think of it as the eight corners of a box.
Q: How many faces does a cuboid have?
A: A cuboid has six faces. These are the flat surfaces that make up the box.
Q: Can a vertex have more than three edges meeting at it?
A: Yes, it’s possible. Think about a pyramid. The apex of the pyramid is a vertex where multiple edges meet, depending on the number of sides of the pyramid’s base.
Q: What is the formula for calculating the volume of a cuboid?
A: The volume of a cuboid is calculated by multiplying the length, width, and height. So, the formula is Volume = Length x Width x Height.
Q: Why is this important for understanding geometry?
A: Understanding the relationships between vertices, edges, and faces allows you to analyze and solve problems related to surface area, volume, angles, and other geometric properties of three-dimensional shapes.
Q: Can I use this information to build something?
A: Absolutely! Knowing the properties of a cuboid can be helpful for projects involving design, construction, or even just understanding how things are put together.
I hope this breakdown has shed some light on how many edges of a cuboid meet at a vertex. Keep exploring the world of geometry and you’ll find there’s much more to discover!
Vertices, Faces And Edges – BYJU’S
The formal definition for the vertex meaning in Maths is defined as a point where two or more edges meet. Vertices are the corner points. Cubes BYJU’S
Cuboid Faces Edges and Vertices (Corners) – YouTube
230. 37K views 2 years ago. This is an educational video about faces, edges and vertices of a cuboid. If you found the video useful, like and subscribe to get YouTube
Cuboid – Definition, Shape, Formulas, Properties,
A cuboid has 6 faces, 12 edges and 8 vertices; The faces of the cuboid are all rectangular in shape; Opposite edges of the cuboid are parallel to each other; Cuboid has three dimensions: length, width and BYJU’S
How many Vertices, Faces, and Edges does a Cuboid have?
Answer: A cuboid has six faces, eight vertices, and twelve edges. Let’s break this down: Vertices: A vertex is a point where two or more lines or edges meet. In GeeksForGeeks
Cuboid – Math.net
Also, an edge of a cuboid is a line segment formed by the intersection of two adjacent faces while a vertex of a cuboid is the point of intersection of three edges. How many faces does a cuboid have? A cuboid has 6 Math.net
Cuboid – Shape, Formula, Meaning, Examples
12 edges: It has 12 edges that include 8 edges of the top and bottom faces and 4 edges that connect them. 8 vertices: It has 8 vertices which are the vertices of the top and bottom faces. At each vertex, three segments Cuemath
Vertices, Faces and Edges – Definition, Example
What are Vertices? What are Faces? What are Edges? Solved Examples. Practice Problems. Frequently Asked Questions. What Are Vertices, Faces, Edges? Every geometric shape is composed of different parts such as SplashLearn
Cuboid – Definition, Shape, Formulas, Properties, Examples
Vertices refer to the corner points. The vertices are joined by the edges. The flat surface bounded by the edges is called the face of a solid. Cuboid has 6 faces, 12 edges, and SplashLearn
Faces, Edges And Vertices – GCSE Maths – Steps
Edges are straight lines that define the sides of the polygons that make up each face of the shape. Vertices (or corners) are points where at least three edges meet. To calculate the number of faces, edges and vertices of a Third Space Learning
Cuboid Faces Edges And Vertices (Corners)
Faces, Edges, And Vertices | How To Identify And Count | Polyhedra | Geometry | Math With Mr. J
How Many Faces, Edges And Vertices Does A Cube Have?
Demonstrative Video – 6 // Visualization Of Faces , Corner And Edges Of A Cuboid
How Many Faces, Edges, And Vertices Does A Cube Have? | Geometry | Math With Mr. J
How To Work Out Sides, Vertices, Faces Of A Cuboid (Egdes, Corners, Surfaces).
Learn About Faces, Edges And Vertices – 3D Shapes | Basic Geometry For Kids | Noodle Kidz
Link to this article: how many edges of a cuboid meet in a vertex.
See more articles in the same category here: https://linksofstrathaven.com/how
