How To Find The Inradius Of A Right Triangle

Finding the inradius of a triangle is pretty straightforward! You can calculate it using a simple formula: r = A/s

Where:

r is the inradius (the radius of the circle inscribed inside the triangle)
A is the area of the triangle
s is the semi-perimeter of the triangle (half of the perimeter)

Let’s break this down a bit further.

Understanding the Inradius

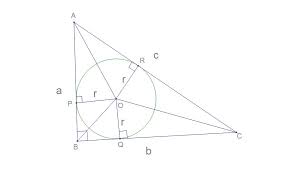
The inradius is the radius of the circle that fits perfectly inside a triangle, touching all three sides. This circle is called the incircle. Imagine drawing a circle inside a triangle so that the circle touches each side of the triangle at exactly one point. The distance from the center of this circle to any of the sides is the inradius.

Calculating the Area (A)

To find the area of the triangle, you can use any of the standard formulas, such as:

A = (1/2) * base * height (where you use the base and corresponding height of the triangle)
Heron’s Formula: A = √(s(s-a)(s-b)(s-c)) where *a*, *b*, and *c* are the side lengths of the triangle and *s* is the semi-perimeter.

Calculating the Semi-Perimeter (s)

The semi-perimeter is simply half the perimeter of the triangle. You find it by adding up the lengths of all three sides and then dividing by two:

s = (a + b + c) / 2

Putting it Together

Once you’ve calculated the area (A) and semi-perimeter (s), simply plug them into the formula r = A/s to get the inradius (r) of the triangle.

Let’s dive into the fascinating world of right triangles and their incircles!

You might be wondering, “What is the radius of the incircle of a right triangle?”. Well, it’s a simple formula, and we can derive it in a way that’s easy to understand.

If the hypotenuse is c and the two legs are a and b, then the inradiusr can be calculated using this formula:

r = (a + b – c) / 2

Now, let’s see how this formula came to be:

The inradius of a triangle is the radius of the circle that is inscribed inside the triangle. This inscribed circle is tangent to all three sides of the triangle. The formula for the inradius is given by r = Area / s, where Area is the area of the triangle and s is the semi-perimeter (half the perimeter).

For a right triangle, we can use the fact that the area of a triangle is (1/2) * base * height and that the semi-perimeter is (a + b + c) / 2.

Let’s substitute these values into the inradius formula:

r = (1/2) * a * b / (a + b + c) / 2

Simplifying the equation, we get:

r = a * b / (a + b + c)

Now, let’s get back to the formula r = (a + b – c) / 2. We can prove this formula is equivalent to the previous formula by showing that they are equal.

To show this, we can multiply both sides of the equation r = (a + b – c) / 2 by (a + b + c):

r * (a + b + c) = (a + b – c) * (a + b + c) / 2

Then, we can expand both sides of the equation and simplify:

r * (a + b + c) = (a² + 2ab + b² – c²) / 2

We know that in a right triangle, a² + b² = c², so we can substitute this into the equation:

r * (a + b + c) = (2ab) / 2
r * (a + b + c) = ab

Dividing both sides by (a + b + c), we get:

r = ab / (a + b + c)

Therefore, we have shown that the two formulas for the inradius are equivalent.

Remember, this formula for the inradius of a right triangle is a valuable tool for solving various geometry problems. So keep it handy!

Let’s talk about finding the inradius of a right-angled triangle, which is the radius of the circle that fits perfectly inside the triangle. You can calculate this using a simple formula: r = ( P + B – H ) / 2. In this formula, r represents the inradius, P stands for the perimeter of the triangle, B is the base, and H represents the height of the triangle.

But where does this formula come from? Let’s break it down. The inradius of a right-angled triangle is actually related to the area of the triangle and its perimeter. Imagine dividing the right-angled triangle into three smaller triangles. Each of these smaller triangles has one of the triangle’s sides as its base and the inradius as its height. The area of the whole triangle is then the sum of the areas of these three smaller triangles.

This means that the area of the triangle is equal to (1/2) r P, where r is the inradius and P is the perimeter. We also know that the area of a triangle can be calculated as (1/2) B H, where B is the base and H is the height. Equating these two formulas, we get (1/2) r P = (1/2) B H. Simplifying, we get r P = B H. Now, solving for r, we get r = (B * H) / P.

But wait, the formula we mentioned earlier was r = (P + B – H) / 2. How do these two formulas relate? Well, the perimeter of a right-angled triangle is simply the sum of its three sides: P = B + H + √(B² + H²). Substituting this value of P into our previous formula, r = (B * H) / P, we get r = (B * H) / (B + H + √(B² + H²)). Now, if we multiply the numerator and denominator of this fraction by (B + H – √(B² + H²)), we get r = (B * H) * (B + H – √(B² + H²)) / ((B + H)² – (B² + H²)). Simplifying this, we arrive at r = (B * H) * (B + H – √(B² + H²)) / (2 * B * H). Finally, canceling out the common factor of B * H from the numerator and denominator, we get r = (B + H – √(B² + H²)) / 2.

So, there you have it! This formula is derived from the relationship between the inradius, area, and perimeter of a right-angled triangle. Using this formula, you can easily calculate the inradius of any right-angled triangle, given its base and height.

Let’s talk about the inradius of a triangle! It’s a pretty cool concept, and it helps us understand some interesting properties of triangles.

The inradius of a triangle is the radius of the circle that can be inscribed inside the triangle, touching all three sides. It’s kind of like fitting the biggest possible circle inside the triangle!

We can find the inradius of a right triangle using a neat formula. Here’s the deal:

In a right triangle ABC, where the right angle is at B, the inradius is (AB + BC – AC)/2.

This formula basically says that the inradius is half the sum of the lengths of the two shorter sides (AB and BC) minus the length of the hypotenuse (AC).

Let’s break down why this works! Imagine drawing a circle inside the right triangle. The circle will touch each side of the triangle at a point. If you draw lines from the center of the circle to these points of contact, you’ll create three smaller triangles. These smaller triangles are all right triangles, and they share the same inradius as the original triangle. The inradius is the height of each of these smaller triangles.

Now, the sum of the lengths of the bases of these smaller triangles is equal to the perimeter of the original triangle (AB + BC + AC). And since the inradius is the height of each smaller triangle, the area of each smaller triangle is (1/2) * base * inradius.

Putting it all together, the area of the original triangle is equal to the sum of the areas of the three smaller triangles. This gives us the equation:

(1/2) * AB * inradius + (1/2) * BC * inradius + (1/2) * AC * inradius = (1/2) * (AB + BC + AC) * inradius.

Simplifying this equation, we get:

inradius = (AB + BC – AC) / 2.

So, there you have it! The inradius of a right triangle is half the sum of the lengths of the two shorter sides minus the length of the hypotenuse. Pretty neat, huh?

You can also use Euler’s Theorem to find the circumradius. This theorem states a relationship between the circumradius (R), inradius (r), and the distance between the incenter and circumcenter (d). The formula is: d² = R(R – 2r).

Let’s break down this formula and understand what it means.

Circumradius (R): The radius of the circle that passes through all three vertices of the triangle. This circle is called the circumcircle.
Inradius (r): The radius of the circle that is tangent to all three sides of the triangle. This circle is called the incircle.
Distance between the incenter and circumcenter (d): This is the straight line distance between the center of the incircle and the center of the circumcircle.

Essentially, Euler’s Theorem connects these three elements. It tells us that the square of the distance between the incenter and circumcenter is equal to the circumradius multiplied by the difference between the circumradius and twice the inradius.

Using Euler’s Theorem:

To use Euler’s Theorem, you’ll need to know either:

1. The inradius (r) and circumradius (R): If you have these values, you can directly calculate the distance (d) between the incenter and circumcenter.

2. The inradius (r) and distance (d): You can rearrange the formula to solve for the circumradius (R): R = (d² + 2dr) / 2d

3. The circumradius (R) and distance (d): You can rearrange the formula to solve for the inradius (r): r = (R² – d²) / 2R

Example:

Let’s say you know the inradius (r) is 3 units and the circumradius (R) is 5 units. Using Euler’s Theorem, you can find the distance (d) between the incenter and circumcenter:

d² = R(R – 2r)
d² = 5(5 – 2 * 3)
d² = 5 ( -1 )
d² = -5

Since the distance cannot be negative, there must be an error in our calculation. This is an example of how Euler’s Theorem can help you check your work and ensure you’re working with accurate measurements.

In Summary:

Euler’s Theorem provides a valuable relationship between the inradius, circumradius, and the distance between the incenter and circumcenter. It can be used to calculate any of these values if you know the other two. This formula is particularly useful in problems where you are given information about the incircle and circumcircle of a triangle, and you need to determine the relationship between these two circles.

Let’s find the inradius of a 3 4 5 triangle.

We can use the formula r = A/s, where r is the inradius, A is the area of the triangle, and s is the semiperimeter.

First, we need to find the area of the triangle. The area of a right triangle is (1/2) * base * height. Since we know the sides of our triangle are 3, 4, and 5, we can use 3 and 4 as the base and height, respectively. This gives us an area of (1/2) * 3 * 4 = 6 square units.

Next, we need to find the semiperimeter. The semiperimeter is half the perimeter, which in this case is (3 + 4 + 5)/2 = 6 units.

Now, we can plug our values into the formula: r = A/s = 6/6 = 1 unit.

Therefore, the inradius of a 3 4 5 triangle is 1 unit.

Let’s break down the concept of inradius further:

* The inradius of a triangle is the radius of the incircle, which is the largest circle that can be inscribed within the triangle.
* The incircle is tangent to all three sides of the triangle.
* The inradius can be visualized as the perpendicular distance from the incenter (the center of the incircle) to any side of the triangle.

Understanding the inradius is important in various geometric problems. For example, it helps us calculate the area of a triangle using the formula A = rs, where r is the inradius and s is the semiperimeter. It also plays a crucial role in determining the relationship between the inradius, circumradius, and semiperimeter of a triangle.

In the case of our 3 4 5 triangle, we have a simple and elegant solution, as the inradius is 1 unit. This means the incircle touches all three sides of the triangle at a distance of 1 unit from the incenter. This understanding helps us visualize and analyze various properties of this right-angled triangle.

Let’s talk about finding the circumradius of a right-angled triangle. It’s actually pretty simple! The circumcenter of a right-angled triangle lies on the midpoint of the hypotenuse. And the circumradius is equal to half of the length of the hypotenuse.

Think of it this way: the circumcenter is the center of the circle that passes through all three vertices of the triangle. Since the hypotenuse is the diameter of this circle, the circumradius is just half of the hypotenuse.

Let’s break this down further:

Circumcenter: This is the point where the perpendicular bisectors of all three sides of the triangle intersect. In a right-angled triangle, this point is always on the midpoint of the hypotenuse.
Hypotenuse: This is the longest side of the right-angled triangle and is opposite the right angle.
Circumradius: This is the radius of the circle that passes through all three vertices of the triangle.

So, to find the circumradius of a right-angled triangle, you simply need to find the length of the hypotenuse and divide it by 2.

Here’s a simple example:

Let’s say you have a right-angled triangle with sides of length 3, 4, and 5 (where 5 is the hypotenuse). To find the circumradius, you would divide the length of the hypotenuse (5) by 2. This gives you a circumradius of 2.5.

Let’s talk about the inradius of an equilateral triangle!

You’re probably wondering how to find the inradius, right? Well, there’s a neat relationship between the inradius (r) and the circumradius (R) of an equilateral triangle. The ratio of the circumradius to the inradius is always 2. This means that R/r = 2 for any equilateral triangle.

Let’s break it down. Imagine an equilateral triangle with a circumcircle (a circle that passes through all three vertices of the triangle). The center of this circumcircle is also the center of the incircle (a circle that touches all three sides of the triangle). The radius of the circumcircle is the circumradius (R), and the radius of the incircle is the inradius (r).

The formula for the inradius of an equilateral triangle is r = (a√3)/6, where a is the length of a side of the triangle. This formula is derived using the relationship between the circumradius, inradius, and the side length of an equilateral triangle.

Let’s say you know the circumradius of an equilateral triangle is 12 cm. Since R/r = 2, we can find the inradius by dividing the circumradius by 2: r = 12 cm / 2 = 6 cm.

So, if you know the circumradius of an equilateral triangle, you can easily calculate the inradius. Just remember the golden ratio: R/r = 2.

Let’s talk about how to find the inradius of a triangle.

First, imagine dividing each of the three angles of the triangle in half. The point where these three lines meet is the center of the incircle. The inradius is a line drawn from this center that touches a side of the triangle at a right angle.

For a right triangle, the inradius (r) has a simple formula: (P + B – H)/2. Here, P is the perimeter of the triangle, B is the base, and H is the height of the triangle.

Let’s break down how this formula works:

The perimeter (P): The perimeter of a triangle is the total length of all its sides. So, for a right triangle, P = base + height + hypotenuse.
The base (B) and height (H): These are the two sides that form the right angle of the triangle.
The inradius (r): The inradius is the radius of the circle that fits perfectly inside the triangle, touching all three sides.

Why does this formula work?

The inradius is connected to the area and perimeter of the triangle in a special way. The area of a triangle is equal to half the product of its perimeter and inradius: Area = (1/2) * P * r.

For a right triangle, the area is also given by (1/2) * base * height. If we set these two area formulas equal to each other, we can solve for the inradius:

(1/2) * P * r = (1/2) * B * H

Simplifying, we get: r = (B * H) / P.

Now, if we substitute P = B + H + hypotenuse, we get:

r = (B * H) / (B + H + hypotenuse)

Finally, we can simplify this expression to get the formula for the inradius of a right triangle: r = (P + B – H)/2.

Let’s try an example:

Imagine a right triangle with a base of 6, a height of 8, and a hypotenuse of 10.

1. Find the perimeter: P = 6 + 8 + 10 = 24
2. Apply the formula: r = (24 + 6 – 8)/2 = 16/2 = 8

Therefore, the inradius of this right triangle is 8.

Remember, this formula works specifically for right triangles. For other types of triangles, the formula for the inradius is a bit more complex.

Let’s dive into the world of triangles and discover how to find their inradius.

The inradius of a triangle is the radius of the circle that fits perfectly inside the triangle, touching all three sides. It’s a neat concept, and there’s a simple formula to calculate it.

To find the inradius, we first need to know the triangle’s area. We can use Heron’s Formula to calculate the area of a triangle if we know the lengths of its sides.

Heron’s Formula states:

Area (K) = √s(s-a)(s-b)(s-c)

Where:

s is the semi-perimeter of the triangle, which is half the perimeter: s = (a + b + c) / 2
a, b, and c are the lengths of the triangle’s sides.

Once we’ve calculated the area (K) using Heron’s Formula, we can use the following formula to find the inradius (r):

r = K / s

This formula tells us that the inradius is equal to the area of the triangle divided by its semi-perimeter.

Let me illustrate this with an example. Suppose we have a triangle with sides of length 3, 4, and 5.

1. Calculate the semi-perimeter (s):
* s = (3 + 4 + 5) / 2 = 6

2. Calculate the area (K) using Heron’s Formula:
* K = √6(6-3)(6-4)(6-5) = √6 * 3 * 2 * 1 = √36 = 6

3. Calculate the inradius (r):
* r = K / s = 6 / 6 = 1

Therefore, the inradius of this triangle is 1.

The inradius is a useful measure in geometry and has applications in various fields like engineering and architecture.

Let’s dive into the fascinating world of right triangles and their inradius. You might be wondering, “How do I find the inradius of a right triangle?”. Let’s explore this together.

If you have a right triangle, the inradius is calculated using the formula r = (a + b − c) / 2, where c represents the hypotenuse and a and b are the legs of the triangle. This formula is a powerful tool for tackling geometric problems and exploring the relationships between Pythagorean triples and the inradius.

But how can we derive this handy formula? Let’s break it down.

Imagine drawing the incircle within the right triangle. The incircle is a circle that touches all three sides of the triangle internally. The inradius is the radius of this incircle. Connecting the center of the incircle to each vertex of the triangle forms three smaller triangles.

These smaller triangles share a special characteristic – they are all right-angled triangles with the inradius as one leg. This is because the tangents drawn from a point outside a circle to the circle are equal in length.

Now, let’s focus on the area of the original right triangle. The area of a triangle is calculated as (base * height) / 2. In our right triangle, the base and height are the legs a and b, so the area is (a * b) / 2.

But we can also calculate the area of the right triangle by summing the areas of the three smaller triangles formed by the incircle. Each of these smaller triangles has a base equal to a side of the right triangle and a height equal to the inradius, r.

So, the area of the right triangle can also be expressed as: (a * r) / 2 + (b * r) / 2 + (c * r) / 2.

Setting these two expressions for the area equal to each other:

(a * b) / 2 = (a * r) / 2 + (b * r) / 2 + (c * r) / 2

Now, let’s solve for r:

(a * b) = (a * r) + (b * r) + (c * r)

(a * b) = r * (a + b + c)

r = (a * b) / (a + b + c)

Finally, using the fact that a² + b² = c² (the Pythagorean theorem), we can simplify the expression:

r = (a * b) / (a + b + c)

r = (a * b) / (a + b + √(a² + b²))

r = (a * b) * (a + b – √(a² + b²)) / ((a + b)² – (a² + b²))

r = (a * b) * (a + b – √(a² + b²)) / (2 * a * b)

r = (a + b – √(a² + b²)) / 2

r = (a + b – c) / 2

And there you have it! This derivation shows that the inradius of a right triangle is indeed r = (a + b − c) / 2. This formula is a valuable tool for problem-solving in geometry and is directly connected to the fundamental principles of triangles, circles, and the Pythagorean theorem.

You can’t actually find the radius of a triangle, because triangles don’t have a radius. However, you can find the inradius, which is the radius of the circle that fits perfectly inside the triangle, touching all three sides.

To find the inradius, you can use this formula: r = A / s, where A is the area of the triangle, and s is the semi-perimeter of the triangle (half of the perimeter).

Let’s break this down:

Area (A): You can find the area of a triangle using various methods, depending on the information you have. For example, if you know the base and height, the area is (base * height) / 2. Or, if you have all three sides, you can use Heron’s formula.
Semi-perimeter (s): This is simply the sum of all three sides of the triangle, divided by 2.

Let’s look at an example:

Imagine you have a triangle with sides of length 5, 12, and 13.

1. Calculate the semi-perimeter (s): (5 + 12 + 13) / 2 = 15
2. Calculate the area (A): You can use Heron’s formula for this, which is: √(s(s-a)(s-b)(s-c)), where a, b, and c are the side lengths. In this case, it would be √(15(15-5)(15-12)(15-13)) = √(15 * 10 * 3 * 2) = √900 = 30.
3. Calculate the inradius (r): r = A / s = 30 / 15 = 2.

So, the inradius of this triangle is 2.

This formula is useful when you’re dealing with geometric problems involving triangles and circles. It lets you find the size of the circle that fits snugly inside a given triangle.

Let’s dive into finding the inradius of a triangle. You can think of the inradius as the radius of the circle that fits perfectly inside the triangle, touching each of its sides.

To find the inradius, we start by drawing the angle bisectors of each of the triangle’s angles. Angle bisectors are lines that divide each angle into two equal angles. These angle bisectors will intersect at a single point called the incenter. This incenter is special because it is *equidistant* from all three sides of the triangle. The distance from the incenter to any side of the triangle is the inradius.

Let’s break down how this works:

1. Angle Bisectors: We begin by drawing lines that divide each angle of the triangle in half. These lines are called angle bisectors.
2. Incenter: The angle bisectors will intersect at a single point. This point is the incenter of the triangle.
3. Inradius: The incenter is a very special point because it’s the same distance from every side of the triangle. This distance is called the inradius. It’s basically the radius of a circle that fits snugly inside the triangle and touches all three sides.

This concept is closely related to the incircle of a triangle. The incircle is the circle that fits perfectly inside the triangle and touches all three sides. The inradius is the radius of the incircle.

Here’s a simple way to think about it: imagine you’re trying to fit a circular cookie inside a triangular cookie cutter. The incircle is the biggest cookie you can fit inside the cutter, and the inradius is the radius of that cookie.

You can use this understanding to find the inradius of any triangle. Just remember to draw the angle bisectors and locate the incenter. The distance from the incenter to any side of the triangle is the inradius.

The inradius of a 3, 4, 5 right triangle is indeed 1. This means that the distance from the incenter (the center of the inscribed circle) to each side of the triangle is equal to 1. This is a neat result and a great example of how geometry can be used to find interesting relationships between different parts of a triangle.

Let’s break down why this is true. The incenter of a triangle is the point where the angle bisectors of the triangle intersect. The inradius is the radius of the circle that is inscribed within the triangle, meaning the circle touches all three sides of the triangle.

In a right triangle, the incenter is always located at the midpoint of the hypotenuse. This is because the angle bisectors of the two acute angles in a right triangle always intersect at the midpoint of the hypotenuse.

In a 3, 4, 5 right triangle, the hypotenuse is 5. Therefore, the incenter is located at a distance of 2.5 from each of the legs (the shorter sides of the right triangle). Since the inradius is the distance from the incenter to each side of the triangle, the inradius in this case is 2.5 – 2 = 1.

We can also find the inradius of a right triangle using the formula:

inradius = (area of triangle) / (semiperimeter of triangle)

The area of a 3, 4, 5 right triangle is (1/2) * 3 * 4 = 6. The semiperimeter is (3 + 4 + 5)/2 = 6. Therefore, the inradius is 6/6 = 1.

So, the inradius of a 3, 4, 5 right triangle is 1, and we can calculate this using either the geometric properties of the incenter or a simple formula.

How do you derive that the inradius in a right triangle is

If we have a right triangle then the inradius is equal to r = a + b − c 2, where c is the hypothenuse and a and b are the legs. This formula is mentioned in various places and it can be useful both in geometric Mathematics Stack Exchange

Inradius of a Right Triangle (visual proof) – YouTube

This is a short, animated visual proof of two different formulas for the inradius of a right triangle in terms of its side lengths. #manim #math #mathvideo #… YouTube

Inradius – Art of Problem Solving

Also the inradius of a incircle inscribed in a right triangle is as by drawing three inradiuses to the three tangent points, then A to that tangent point is equal to A to the other Art of Problem Solving

Inradius, Semiperimeter, and Area – Expii

Inradius can be calculated with the following equation: r=As Where A is the area of the triangle, and s is the semi-perimeter of the triangle, or one-half of the perimeter. You can Expii

Inradius — from Wolfram MathWorld

The inradius of a regular polygon with n sides and side length a is given by r=1/2acot(pi/n). (1) The following table summarizes the inradii from some nonregular Wolfram MathWorld

Triangle Incircle Calculator: Radius, Area, and Ratio

The Triangle Incircle Calculator is a tool that allows you to determine the properties of the incircle of a triangle based on its side lengths. By entering the lengths of the three sides, Online calculators

Right Triangle — from Wolfram MathWorld

A right triangle is triangle with an angle of 90 degrees (pi/2 radians). The sides a, b, and c of such a triangle satisfy the Pythagorean theorem a^2+b^2=c^2, (1) where the largest side is conventionally denoted c and Wolfram MathWorld

Trigonometry/Circles and Triangles/The Incircle – Wikibooks

Calculating the radius. Its radius, the inradius (usually denoted by r) is given by r = K/s, where K is the area of the triangle and s is the semiperimeter (a+b+c)/2 (a, b wikibooks.org

Inradius, perimeter, & area (video) | Khan Academy

If I have a triangle that has lengths 3, 4, and 5, we know this is a right triangle. You can verify this from the Pythagorean theorem. And if someone were to say what is the inradius of this triangle right over here? Well we can figure out the Khan Academy

Incircle (Inscribed circle) of Right, Equilateral and … – YouTube

In this video, we will guide you through the steps to find the inradius of these different types of triangles. By the end of this tutorial, you will have a c… YouTube